[용어/개념] 멧칼프의 법칙(Metcalfe's Law)/암달의 법칙(Amdal's Law)/무어의 법칙(Moore's Law) 비교

멧칼프의 법칙 (Metcalfe’s Law)

I. 네트워크의 효용성, 멧칼프 법칙의 개요

가. 멧칼프(Metcalfe) 법칙의 정의

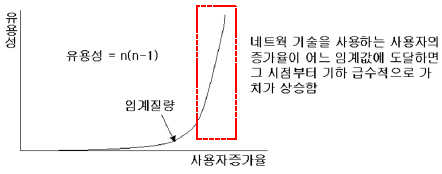
• 하나의 네트워크의 유용성 또는 효용성은 그 네트워크 사용자의 제곱에 비례한다는 법칙

나. 멧칼프 법칙의 효용성의 의미

• 사용자 환경이 PC 중심에서 네트워크 중심으로 이동(인터넷의 발달에 의함)
• 네트워크의 성장 속도를 잘 설명하는 법칙
• 멀티미디어 등을 실어 나를 인터넷의 중요성 뒷받침

II. 멧칼프 법칙의 특징

가. 멧칼프 법칙의 개념도

[사례] 인터넷의 사용, SNS

 

나) 멧칼프 법칙과 무어의 법칙 비교(무어의 법칙에서도 공통으로 사용)\

구분	멧칼프의 법칙	무어의 법칙
대상	네트워크 유용성 및 사용자 증가율	마이크로 칩의 처리능력과 시간
Since	1981년 3Com의 멧칼프	1965년 인텔의 고든 무어
적용사례	전화의 보급	인텔의 Micro processor 개발 주기
시사점	인터넷이 킬러 앱으로 점점 더 폭발적인 위력을 가질 것이라는 것을 보여줌	디지털 시대에 컴퓨터가 보다 쉽게 보급되어 킬러 앱이 되는 이유를 설명

 

 

III. 지식기반사회의 적용

가. 무어의 법칙

• 많은 사람들이 적은 비용으로 컴퓨터를 사용할 수 있게 됨
• 컴퓨터에 의한 지식기반 사회가 빠르게 확산됨을 증명

나. 멧칼프의 법칙

• 모든 컴퓨터가 인터넷을 통하여 연결되어 네트워킹의 확장이 가속화될 것을 예견
• 정보의 생성, 공유 등을 통한 지식기반 사회의 가치가 커짐을 증명
• 새로운 비즈니스 모델과 글로벌 협업의 시대가 열렸음을 의미

---

반응형

암달의 법칙 (Amdal's Law)

 

I. 프로세스 병렬화 속도 한계성에 대한 암달의 법칙

가. 암달(Amdahl)의 법칙 정의

• 프로그램은 병렬처리가 가능한 부분과 불가능한 순차적인 부분으로 구성되므로 프로세서를 아무리 병렬화 시켜도 더 이상 성능이 향상되지 않는 한계가 존재한다는 법칙

나. 암달의 법칙 의미

• 성능 한계는 캐시, 메모리, 버스와 같이 제한된 자원을 프로세스가 서로 점유하려고 쟁탈하는 오버헤드에 이해 발생
• 시스템 구성상 프로세서가 2배가 되더라도 20~40% 정도의 성능 손실이 발생, 4개의 CPU를 쓰더라도, 단일 CPU에 비해서 평균 2.5배 정도 성능 향상
• 병렬처리 컴퓨터를 효율적으로 사용하기 위해서는 순차처리코드 부분이 적어야 함.
• 순차처리 코드비율이 크면 프로세서 수가 증가해도 성능향상 및 속도개선이 안됨

 

II. 암달의 법칙 개념도

암달의 법칙 개념도

• f : FRACTION [비율] : 순차적으로 수행해야 되는 부분
• 잠재적인 프로그램 Speed Up을 기술하는 Amdahl 법칙은 병렬화 시킬 수 있는 코드의 비율(P)로 정의
• Speedup = 1/(1-P)

 

III. 암달의 법칙 공식 적용 예제

가) 시스템 성능 향상도 구하기(Single CPU))

• 암달의 법칙은 성능 향상 변수를 측정하여 파악하고 성능 향상과 상관관계를 분석하여 시스템 설계에 반영해야 함.

시스템 성능 향상도 구하기

• n : 향상배수, t : 향상 가능 부분
• 프로그램 A 샘플

프로그램 A 샘플

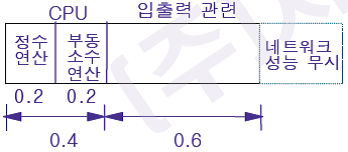
* 사례 A (상용업무 전반) : CPU Clock Speed 2배 가속

사례 A (상용업무 전반)

 

* 사례 B (공학계산) : 부동소수연산 가속기 부착 2배 가속

 

사례 B (공학계산)

* 사례 C (거의 모든 상용업무) : 메모리/디스크 입출력 2배 향상(-> Bus 구조, 캐시, 디스크 등 시스템 아키텍처 최적화)

사례 C (거의 모든 상용업무)

 

 

나) 코드의 병렬화만 개선 시 성능 향상도

코드의 병렬화만 개선시 성능 향상도

 

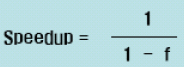
f : fraction of code which can be parallelized

• f가 0%(0.0)인 경우 speedup = 1 즉, 속도 향상 없음
• f가 50%(0.5)인 경우 speedup = 2 즉, 2배 향상
• f가 80%(0.8)인 경우 speedup = 5 즉, 5배 향상
• f가 90%(0.9)인 경우 speedup = 10 즉, 10배 향상
• f가 Near 100%인 경우 speedup = 무한대 (이론상)

fraction of code which can be parallelized

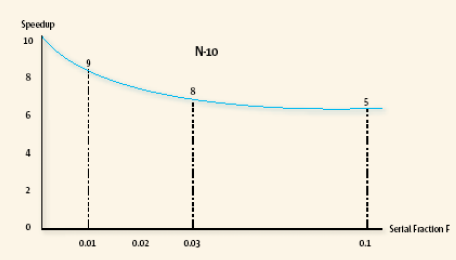
• 코드의 병렬화가 100%인 경우 시스템의 속도는 무한대 향상되지만 실제 구현은 불가능

 

다) 코드와 프로세서의 수를 함께 개선하는 경우 성능 향상도

성능 향상도

 

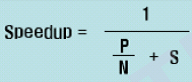
P : Parallel fraction, N : Process의 수, S : Serial Fraction

• Serial Fraction의 경우 프로세서를 늘려도 성능 향상의 의미가 없음
• Parallel Fraction의 경우 프로세서의 수와 병렬화 정도에 따라 성능 향상이 가능

Parallel fraction

 

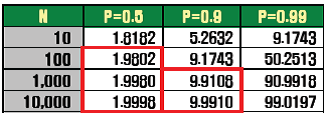
- P + S = 1 이므로 P가 0.5인 경우 S는 0.5로 간주
- P가 50% 인 경우 프로세서가 100개인 경우와 10,000개인 경우 간의 성능향상이 거의 없음
- P가 90% 인 경우 프로세서가 1,000개인 경우와 10,000개인 경우 간의 성능향상이 거의 없음

Parallel fraction

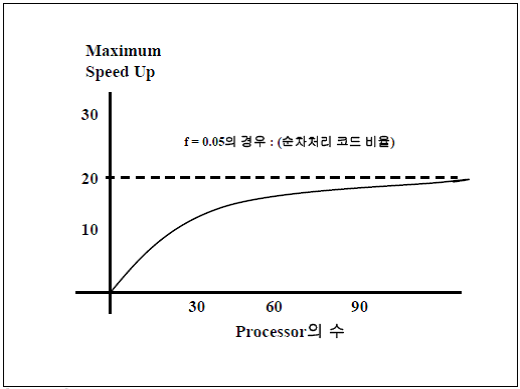
• 프로세서 수가 증가해도 성능 향상 및 속도 개선은 한계가 있음

 

 

IV. 암달의 법칙을 이용한 CPU 성능향상 방안

 

가) 순차처리 코드의 오버헤드 극복

• 프로그램에서 데이터 초기화 (I/O)는 병렬화가 어려움
• 프로그램의 계산량은 데이터 크기의 지수승에 비례

* Rank Sort : n2에 비례, O(n2), 제곱승

* 행렬 곱셈 : n3에 비례, O(n3), 세제곱승

• 암달의 법칙에서 데이터 초기화를 위한 순차처리 코드 부분에 의한 성능저하는 데이터 크기를 증가함으로써 극복함 -> 동일한 수천수만의 순차처리 업무를 대단위로 분산처리, 고도의 수치계산, Data Mining, 네트워크 통합 시뮬레이션 등에서 활용됨

나) 병렬처리 기법 적용

• 파이프라인 구조의 시스템아키텍처 설계
• 병렬프로세서 도입
• 프로그램 컴파일 최적화 기법 적용
• 데이터의 의존성 최소화한 응용시스템 개발

 

 

V. Amdahl의 법칙 활용

• 최저 비용으로 최상의 시스템을 구현할 수 있는 수학적 근거로 활용
• 시스템의 성능에 대한 개선을 하드웨어적인 접근 방식이 아닌 OS, 컴파일러, 소프트웨어등과 같은 다양한 분야에서 접근 가능하도록 전기를 마련
• Sun의 경우 JDK 1.4 개발 시 Garbage Collection 성능 향상을 위한 설계에 적용
• OS, 시스템 S/W, 전략적인 고도수치계산 등의 개발 시 분산처리는 기본적인 사항으로 고려됨

 

멧칼프의 법칙	암달의 법칙
네트워크 유용성 및 사용자 증가율	Process 수를 병렬화해도 성능 상상의 한계가 존재한다는 법칙
1981년 3Com의 멧칼프	1967년 Amdahl의 논문에서 발표
전화의 보급	4개 CPU 사용 -> 2.5배의 성능 향상
인터넷이 킬러 앱으로 점점 더 폭발적인 위력을 가질 것이라는 것을 보여줌	프로그램 내에서 데이터 초기화(I/O)는 병렬화가 어렵지만, 분산처리, 고도의 수치계산으로 극복 가능

---

 

반응형

무어의 법칙 (Moore's Law)

 

I. 마이크로칩의 발전 법칙, 무어의 법칙 개요

가. 무어의 법칙(Moore's Law)의 개념

• 마이크로칩의 처리 능력은 18개월마다 2배로 늘어난다는 법칙
• 정보 혁명의 기본 구성요소인 마이크로 칩의 가격은 18개월마다 절반으로 하락한다는 의미의 법칙
• 1965년 페어차일드(Fairchild)의 연구원으로 있던 고든 무어(Gordon Moore)가 경험적인 관찰에 바탕을 두고 마이크로칩의 용량이 매년 2배가 될 것으로 예측하며 만든 법칙으로, 1975년 24개월로 수정되었고, 그 이후 18개월로 정의

 

II. 무어의 법칙 개념도 및 의미

가. 무어의 법칙 개념도

무어의 법칙 개념도

 

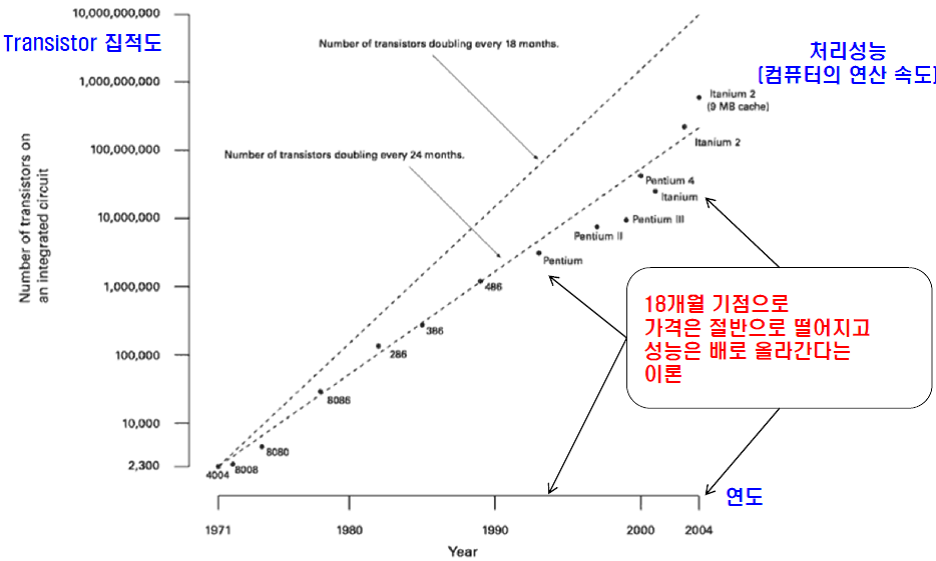
나. 무어의 법칙에서 “2배”의 의미

비용 절감	-'더 빠르게, 더 작게, 더 싸게'라는 의미. - 무어의 법칙 하에서 칩 설계자들은 지금은 나노미터 단위인 트랜지스터의 크기를 줄여가고 있고 결과적으로 칩의 빈 공간에 트랜지스터를 더 많이 담아내고 있다. 트랜지스터의수가 더 많아지면 칩 설계자들은 이전에는 분리된 칩이었던 3차원그래픽 같은 더 많은 기능을 여분의 공간을 이용해 하나의 칩으로 집적 할 수 있게 되는 비용절감 효과
비용과속도의 관계	- 트랜지스터가 점점 작아진다는 말은 전자가 멀리 갈 필요가 없어 성능이 좋아진다는 말

 

 

III. 무어의 법칙 적용 현황 및 한계성 논란

 

가. 무어의 법칙 적용 현황

• 인터넷은 적은 노력으로도 커다란 결과를 얻을 수 있다'는 멧칼프의 법칙, '조직은 계속적으로 거래 비용이 적게 드는 쪽으로 변화한다'는 가치사슬을 지배하는 법칙과 함께 인터넷 경제 3원칙으로 불리고 있음
• 인텔의 창립자인 무어가 한 말인 만큼 인텔에 의해 현재까지 지켜지고 있음.
• 2009년 인텔은 32 나노 및 22 나노 제조 기술의 발전과 함께 무어의 법칙은 지켜졌다는 평가를 받음
• 무어의 법칙은 곧 소멸될 것이라는 예측을 깨고 2010년 3월 미국 MIT의 연구진이 지금까지 보다 훨씬 작은 회로요소를 가진 마이크로프로세서를 만들 수 있는 나노공정기술인“자기 조립(Selg Assembling) 원형칩” 개발에 성공

 

나. 무어의 법칙에 대한 한계성 논란

• 마이크로 칩의 성능은 정해진 적정 면적 내에 얼마큼의 회로를 배열할 수 있는지에 따라 결정됨.
• 18개월 혹은 24개월마다 정해진 실리콘기판에 두 배씩의 회로를 심어야 한다는 무어의 법칙은 결구 물리적인 한계에 봉착하게 될 것이라는 논란이 있음

 

[용어/개념] 파레토의 법칙(Pareto principle) / 길더의 법칙(Guilder's Law) 정의 및 소개

[용어/개념] 파레토의 법칙(Pareto principle) / 길더의 법칙(Guilder's Law) 정의 및 소개

 

[용어/개념] Network - OSI 7 Layer 기본

[용어/개념] Network - OSI 7 Layer 기본

 

[용어/개념] 생성형 AI 사이트 정리 (추가 업데이트 2024.08)

[용어/개념] 생성형 AI 사이트 정리 (추가 업데이트 2024.08)