[FCF] Technical Introduction - 암호화 및 PKI 모듈 Part 3 ( 해싱, 디지털 서명 )

A. 해싱 개요

1. 해싱이란?

해싱은 임의 크기의 데이터를 고정된 크기의 고유한 값으로 변환하는 프로세스입니다. 해싱에는 암호화를 지원하는 몇 가지 중요한 기능이 있습니다.

 

 

암호화를 지원하는 중요한 기능의 정의는 다음과 같습니다.

 

첫째, 출력 값은 해싱 함수 또는 알고리즘에 의해 결정되는 고정 길이입니다. 주어진 알고리즘에 대해 출력 값은 항상 동일한 크기이기 때문에 악의적인 행위자는 입력 데이터의 크기에 대한 정보가 없습니다. 12자의 비밀번호일 수도 있고 6페이지짜리 문서일 수도 있습니다.

 

둘째, 충돌을 피하기 위해 출력 값은 모든 입력 값에 대해 고유합니다. 이 기능은 데이터 변경 사항을 감지하려는 경우 해싱을 매우 유용하게 만듭니다. 예를 들어 누군가가 전자 문서를 변조한 경우, 작은 변경이라도 원본 문서의 해시 출력과 변경된 문서의 출력을 비교하면 두 출력이 완전히 다르다는 것을 알 수 있으며 경고를 받을 수 있습니다.

 

셋째, 해싱은 되돌릴 수 없거나 단방향으로만 진행됩니다. 즉, 해싱 함수를 통해 출력값을 실행하면 입력값을 얻지 못한다는 뜻입니다. 이 기능은 악의적인 행위자가 출력 값을 사용하여 입력 값을 리버스 엔지니어링하고 계산할 기회를 원천 차단합니다.

 

2. 디지털 서명

해싱의 보안 기능과 비대칭 암호화를 결합하면 디지털 서명을 생성할 수 있습니다. 그리고 해싱의 보안 기능은 디지털 서명 생성 시 암호화에서 중요한 역할을 합니다. 디지털 서명은 다양한 용도로 사용됩니다. 디지털 서명은 서명된 정보의 데이터 무결성을 보장하고 정보에 서명한 사람이나 사물을 인증하며 부인방지를 지원합니다.

 

2-1. 디지털 서명 생성 프로세스

 

첫 번째 단계에서는 서명해야 하는 정보가 해시됩니다. 그러면 출력 해시 값이 생성됩니다.

 

두 번째 단계에서는 서명자와 연결된 비대칭 개인 서명 키가 비대칭 알고리즘을 사용하여 출력 값을 암호화합니다. 이 암호화된 출력 값을 디지털 서명이라고 합니다.

 

세 번째 단계에서는 정보에 디지털 서명이 첨부됩니다.

 

2-2. 디지털 서명 검증 프로세스

 

첫 번째 단계에서 수신자의 애플리케이션은 정보를 해시하여 새로운 출력 값을 생성합니다.

 

두 번째 단계에서는 서명자의 확인 인증서가 유효한지 확인한 후 공개 키가 디지털 서명을 해독(즉, 확인)합니다.

 

세 번째 단계에서 검증자는 새 출력 값을 원래 출력 값과 비교합니다. 동일하다면 정보가 변경되지 않은 것입니다. 공개 키가 디지털 서명을 성공적으로 해독했고 해당 키 소유자의 이름이 인증서에 기록되어 있으므로 서명자의 진위를 확인할 수 있습니다.

 

반응형

 

 

3. 해시 함수의 유형

 

MD5의 다섯 번째 버전은 128비트 해시 출력을 생성합니다. 이 기능은 주로 충돌에 대한 취약성과 같은 약점이 발견될 때까지 널리 사용되었습니다. MD6이 MD5를 대체했습니다.

 

이후 SHA-1이 더 대중화되었고 SHA-2와 SHA-3이 그 뒤를 이었습니다. SHA-1 기능은 160비트 해시 출력을 생성하는 반면 SHA-2는 실제로 해싱 알고리즘 모음입니다. 이 제품군에는 SHA-224, SHA-256, SHA-384 및 SHA-512가 포함되어 있습니다. SHA-3을 사용하면 출력 값의 길이를 결정할 수 있습니다.

 

LANMAN은 레거시 Windows 운영 체제에서 암호를 저장하는 데 사용되었습니다. LANMAN은 안전하지 않은 것으로 입증되었으며 무차별 대입 공격에 의해 무력화될 수 있는 데이터 암호화 표준(DES)을 사용합니다. 해싱 및 디지털 서명 강의 NTLM은 LANMAN의 뒤를 이어 NTLM 버전 2가 이어졌습니다.

 

북미 이외의 지역에서는 HAVAL 및 RIPEMD가 널리 사용되는 해싱 함수입니다.

 

 

4. 해싱에 대한 일반적인 공격

해싱을 크랙 하는 데 사용되는 매우 일반적인 방법은 무차별 대입 공격입니다. 이는 악의적인 행위자가 원래 해시 출력과 동일한 값을 생성할 때까지 다른 입력 값을 시도한다는 것을 의미합니다.

 

공격자가 입력 데이터의 크기를 전혀 모르는 경우 무차별 대입 공격의 성공은 제한적입니다. 그러나 공격자가 입력 값에 대해 알고 있는 경우 적용되지 않는 입력 값을 제거할 수 있습니다.

 

예를 들어 입력 값이 비밀번호이고 악의적인 행위자가 비밀번호 요구 사항을 알고 있는 경우(예: 최소 길이는 10자, 최대 길이는 20자이며 대문자, 소문자 및 숫자를 포함해야 함) 공격 범위를 대폭 좁힐 수 있습니다.

 

또 다른 예로, 해시 출력이 MD5를 사용하여 4자리 PIN을 보호하고 있다는 것을 악의적인 행위자가 알고 있는 경우 동일한 해시 출력에 도달할 때까지 가능한 모든 조합을 시도할 수 있습니다.

 

 

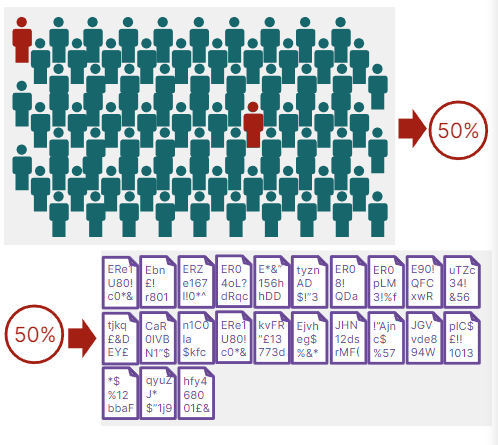
무차별 대입 공격의 한 유형은 생일 역설에 기초하고 충돌을 일으키는 것으로 알려진 해싱 기능을 이용하는 생일 공격입니다.

 

당신이 183명의 사람들과 함께 방에 있었다면, 그중 한 사람이 당신과 생일을 같을 확률은 50%입니다. 그러나 생일이 같은 두 사람이 있을 확률을 50% 원한다면 23명만 있으면 됩니다. 이것이 바로 생일 역설입니다. 해싱 함수의 경우 이는 일치하는 항목 두 개를 찾는 것이 훨씬 쉽다는 것을 의미합니다.

 

 

해시된 비밀번호를 해독하려고 시도할 때 악의적인 행위자는 입력 데이터가 비밀번호와 일치하는지 여부에는 신경 쓰지 않으며 입력 데이터가 동일한 해시 출력을 생성한다는 점만 고려합니다. 이는 서버가 사용자 비밀번호를 저장하지 않기 때문입니다. 그들은 해당 비밀번호의 해시를 저장합니다.

 

따라서 악의적인 행위자가 Alice의 비밀번호를 보호하는 해시 출력을 재현할 수 있으면 Alice로 로그인할 수 있습니다. 앞에서 언급했듯이 두 개 이 상의 입력 값이 동일한 출력 값을 생성하는 상황을 충돌이라고 합니다.

 

생일 공격은 확률 이론의 생일 문제 뒤에 숨은 수학을 이용합니다. 생일 공격의 성공은 주로 무작위 공격 시도와 고정된 순열 정도 사이에서 발견되는 충돌 가능성에 따라 달라집니다. 무차별 대입 공격에 대한 최선의 방어는 해시 함수가 계산상 깨뜨릴 수 없을 만큼 긴 출력을 지원하는지 확인하는 것입니다.

 

비밀번호를 보호하기 위해 해싱을 사용할 때 함수가 충돌에 취약한 경우 해시 출력 값의 길이를 늘이는 것만으로는 충분하지 않을 수 있습니다. 컴퓨터에 저장된 비밀번호 해시를 보호하기 위해 키 스트레칭 과정을 통해 엔트로피를 높일 수 있습니다.

 

 

생일 역설의 수학적 계산을 이해하려면 생일이 같은 사람이 아무도 없을 확률을 계산하고 결과를 뒤집는 것이 더 쉬울 수 있습니다.

 

사람들이 방에 들어올 때 생일을 물어본다고 상상해 보십시오. 그 방에 있는 두 사람의 생일이 같을 확률은 얼마나 됩니까?

 

한 사람이 방에 들어가면 방에 다른 사람이 없기 때문에 다른 사람과 생일을 공유할 가능성이 없습니다. 그러나 두 번째 사람이 방에 들어간 후에는 지금 방에 있는 두 사람의 생일이 같을 확률은 365분의 1이다. 1년은 365일(윤년 생략), 즉 365개의 가능성이 있기 때문에 365가 분모입니다.

 

즉, 이 두 사람이 같은 생일을 공유하지 않을 확률은 364/365입니다.

 

세 번째 사람이 방에 들어올 때 두 번의 생일을 피해야 합니다. 따라서 세 번째 사람이 첫 번째 또는 두 번째 사람과 생일을 공유하지 않을 확률은 363/365입니다. 방에 있는 세 사람 중 생일이 같은 사람이 없을 확률을 확인하려면 마지막 결과에 이 분수(0.9973 x 363/365)를 곱해야 합니다.

 

네 번째 사람이 방에 들어올 때 세 번의 생일을 피해야 합니다. 마지막 결과인 0.9918에 362/365를 곱합니다.

 

23번째 입실자에게 앞서면 피해야 할 23일이 있습니다. 그러므로 같은 생일을 공유하지 않을 확률은 343/365입니다. 그러나 방에 있는 모든 사람을 고려하면 [0.5243 x 343/365] 결과는 놀라운 0.4927입니다.

 

즉, 23명의 방에서 두 사람이 생일이 같지 않을 확률은 약 49%, 생일이 같을 확률은 51%입니다.

 

[FCF] Technical Introduction - 암호화 및 PKI 모듈 Part 2

[FCF] Technical Introduction - 암호화 및 PKI 모듈 Part 2

 

[FCF] Technical Introduction - 암호화 및 PKI 모듈 Part 1

[FCF] Technical Introduction - 암호화 및 PKI 모듈 Part 1