[Algorithm] 계수 정렬 (Counting Sort)

계수 정렬 (Counting Sort) - 개념

선형 시간에 정렬하는 효율적인 알고리즘

 

 

I. 계수 정렬 (Counting Sort)의 개요

가. 계수 정렬의 정의

- 선형 시간에 정렬하는 효율적인 알고리즘

 

반응형

나. 계수 정렬의 특징

- 입력키가 한정될 때 사용가능 (입력이 0부터 K사이의 수)

- 정수나 정수로 표현할 수 있는 자료에 대해서만 동작

- Max 값 산출이 선행되어야 함

 

 

Ⅱ. Algorithm Concept

카운팅 정렬은 다음과 같은 과정으로 수행된다.

1. 입력받은 배열 A의 요소값들의 등장 횟수를 저장할 배열 B와 최종적으로 정렬된 값들을 담을 배열 C를 준비한다.
2. 입력밭은 배열에서 값을 하나씩 꺼내서 해당 값을 배열 B의 인덱스로 사용해 B의 요소 값을 하나 증가시킨다. (B [A [i]]++)
3. B가 완성되면 B의 각 요소들을 누적합으로 갱신한다. B [i] = B[i] + B [i-1]
4. A의 가장 뒤에서부터 값을 하나씩 꺼내서 해당값을 B의 인덱스로 사용하고 참조된 B의 값을 배열 C의 인덱스로 사용해서 배열 C에 A에서 꺼낸 값을 넣는다. C[B[A [i]]] = A[i]
5. 사용된 B의 값을 하나 감소시킨다. (B [A [i]]--)
6. A의 모든 요소에 대해 4번, 5번 과정을 반복한다.

배열이 여러 개 사용되고 서로가 서로를 인덱스로 사용하는 상황이랑 글로는 이해하기가 쉽지 않다. 그림으로 알아보자.

반응형

 

Example

계수 정렬 (Counting Sort)

 

일단 배열 A를 입력받았고, 배열 B와 C를 준비했다.

Phase 1

계수 정렬 (Counting Sort)

 

제일 먼저, A를 순회하면서 A에 들어가 있는 값들의 등장 횟수를 배열 B에 저장해 주었다. 예를 들어 A에서 0이라는 값은 존재하지 않기 때문에 B의 0번 인덱스는 0이 되고, 3은 총 2번 등장했기 때문에 B의 3번 인덱스는 2로 경신되었다.

주목할 점은 B의 배열길이는 A에 있는 최댓값에 따라 결정된다는 것이다. 이후에 이것이 성능에 어떤 영향이 있을지 논의해 보자.

 

Phase 2

계수 정렬 (Counting Sort)

 

B 배열의 값들을 1부터 마지막 값까지 바로 이전 값과 계속 더해서 누적합으로 만들어준다.

 

Phase 3

계수 정렬 (Counting Sort)

1. 배열 A의 가장 뒤에서부터 값을 하나씩 꺼낸다. 이번에 꺼낸 값은 6이기 때문에 이 값을 배열 B의 인덱스로 사용해서 접근한다.
2. 배열 B의 6번 인덱스에 있는 값은 6이기 때문에 이 값을 사용해서 C에 접근한다. 이것은 배열 A에는 6보다 같거나 작은 값이 총 6개가 있음을 의미한다.
3. 배열 C의 6번째 요소에 6을 넣는다. 배열 A에 6보다 같거나 작은 값이 6개 있기 때문에 최종 배열의 6번째 칸에 넣어주면 6보다 작은 값은 모두 이 인덱스의 앞에 위치하고 큰 값들은 뒤에 위치하게 될 것이다.
4. 배열 B의 6번 인덱스의 값을 하나 줄여준다.

 

Phase 4

계수 정렬 (Counting Sort)

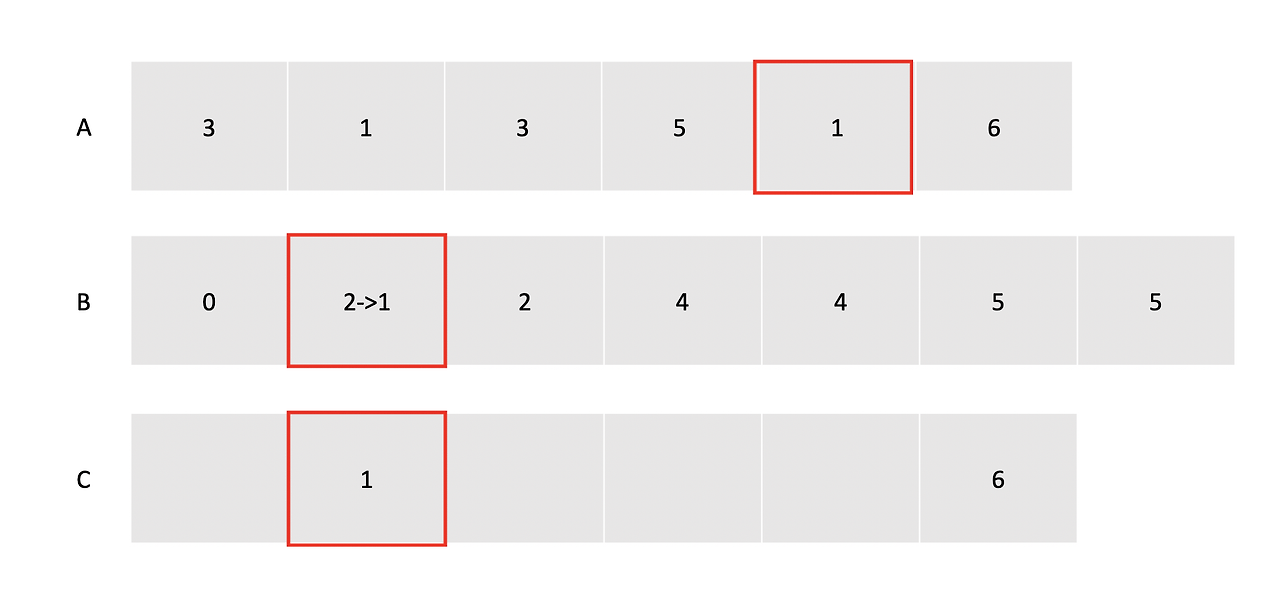
1. A 배열에서 다음 값인 1을 꺼낸다.
2. B 배열의 1번 인덱스에는 2가 들어있기 때문에
3. C 배열의 2번째 위치에 A에서 꺼낸 값인 1을 넣어주고,
4. B 배열의 1번 인덱스의 카운트를 하나 줄여준다.

 

Phase 5

계수 정렬 (Counting Sort)

1. A 배열에서 다음 값인 5를 꺼낸다.
2. B 배열의 5번 인덱스에는 5가 들어있기 때문에
3. C 배열의 5번째 위치에 A에서 꺼낸 값인 5를 넣어주고,
4. B 배열의 5번 인덱스의 카운트를 하나 줄여준다.

 

Phase 6

계수 정렬 (Counting Sort)

1. A 배열에서 다음 값인 3을 꺼낸다.
2. B 배열의 5번 인덱스에는 4가 들어있기 때문에
3. C 배열의 4번째 위치에 A에서 꺼낸 값인 3을 넣어주고,
4. B 배열의 3번 인덱스의 카운트를 하나 줄여준다.

 

Phase 7

계수 정렬 (Counting Sort)

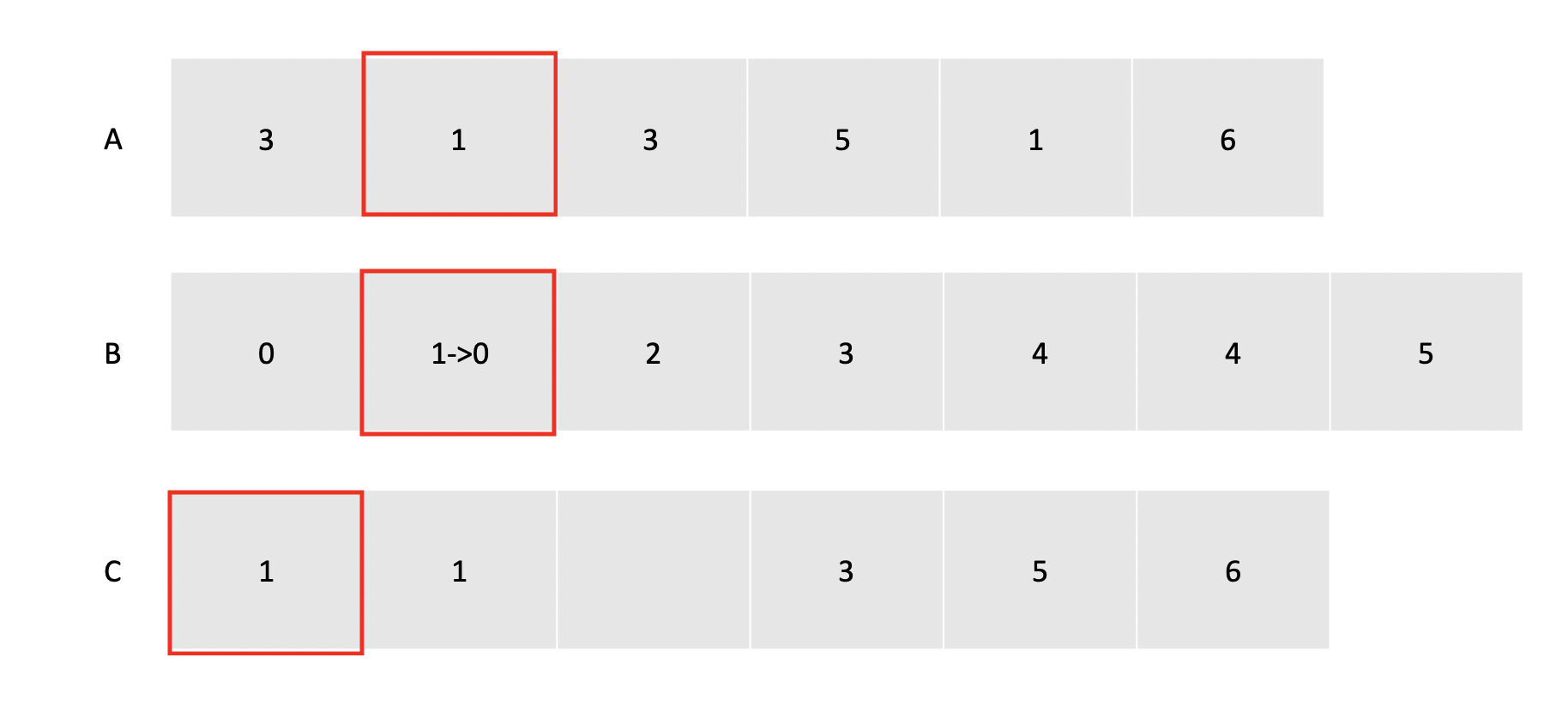
1. A 배열에서 다음 값인 1을 꺼낸다.
2. B 배열의 1번 인덱스에는 1이 들어있기 때문에
3. C 배열의 1번째 위치에 A에서 꺼낸 값인 1을 넣어주고,
4. B 배열의 1번 인덱스의 카운트를 하나 줄여준다.

 

반응형

Phase 8

계수 정렬 (Counting Sort)

1. A 배열에서 다음 값인 3을 꺼낸다.
2. B 배열의 3번 인덱스에는 3이 들어있기 때문에
3. C 배열의 3번째 위치에 A에서 꺼낸 값인 3을 넣어주고,
4. B 배열의 3번 인덱스의 카운트를 하나 줄여준다.

 

Implement

// k == max number
// n == number of data in A
void counting_sort(int A[], int B[], int C[]){
 
    /* 카운팅 배열 0으로 초기화 */
    for (int i = 0 ; i <= k ; i++){
        B[i] = 0;
    }
 
    /* 카운팅 값 갱신  */
    for (int i = 1 ; i <= n ; i++){
        B[A[i]] = B[A[i]] + 1;
    }
 
    /* 누적합 계산 */
    for (int i = 1 ; i <= k ; i++){
        B[i] = B[i] + B[i-1];
    }
 
    /* 결과 배열에 값 넣기 */
    for (int i = n ; i >= n ; i--){
        C[B[A[i]]] = A[i];
        B[A[i]] = B[A[i]] - 1;
    }
}

 

 

Algorithm Analysis

 

앞서 잠깐 언급했던 것처럼 이 알고리즘의 치명적인 단점은 카운팅을 위한 배열의 길이가 입력받은 배열 값들 중 최댓값에 의해 결정된다는 것이다. 만약 우리가 입력받은 배열의 값들이 (1, 100000)이라고 한다면, 이 배열은 두 개의 값만을 가지고 있음에도 불구하고 카운팅 배열의 크기는 100000으로 설정되어야 한다.

 

또한 이 알고리즘의 시간 복잡도는 Օ(n * k)가 되는데, 배열을 참조하는 연산 O(n) 이 B 배열의 길이인 k, 즉 배열 내의 최대 값의 길이만큼 반복되기 때문이다. 따라서 입력받은 배열의 데이터개수가 k 보다 작다면 굉장히 유용한 알고리즘이 되겠지만, k 가 더 큰 경우에는 비효율적인 알고리즘이 될 수도 있다.

 

 

 

[Algorithm] 백트래킹 알고리즘

[Algorithm] 백트래킹 알고리즘

 

 

[용어/개념] AAA(Authentication Authorization Accounting) 프로토콜

[용어/개념] AAA(Authentication Authorization Accounting) 프로토콜