반응형
최소신장트리 알고리즘 - 개 념
최소신장트리 (Minimum Spanning Tree) 알고리즘 (프림 알고리즘, 크루스칼 알고리즘)
모든 정점을 포함하고 정점 간 서로 연결하면서 사이클이 존재하지 않는 그래프
I. 신장트리 (Spanning Tree)의 개요
가. 신장 트리의 정의
- 모든 정점을 포함하고 정점 간 서로 연결하면서 사이클이 존재하지 않는 그래프
나. 최소신장트리의 정의
- 정점 간 가중치(cost)의 합이 최소인 신장 트리
Ⅱ. 최소신장트리 알고리즘
가. Prim의 알고리즘
* 시작점 기반 최소 가중치 * 정점마다 edge 검사 * 우선순위 큐 기반 구현
|
 |
void prim(int n, const number W[][], set_of_edges& F) { index i, vnear; number min; edge e; index nearest[2..n]; number distance[2..n]; F = empty_set; for(i=2;i <= n;i++) { nearest[i] = 1; distance[i] = W[1][i]; } repeat(n-1 times) { min = ; for(i=2; i <= n; i++) { if 0 <= distance[i] < min) { min = distance[i]; vnear = i; }} e = vnear와 nearest[vnear]를 잇는 이음선; e를 F에 추가; distance[vnear] = -1; for(i=2; i <= n; i++) if (W[i][vnear] < distance[i]) { distance[i] = W[i][vnear]; nearest[i] = vnear; }}} |
나. Kruskal의 알고리즘
* 가중치의 오름차순 정렬 수행 * 최소 가중치 edge 선택 * 분리집합 기반 구현
|
||
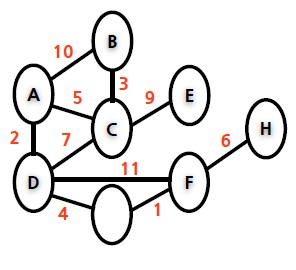 |
⇒ |  |
 |
||
void kruskal( int n, int m, set_of_edges E, set_of_edges& F) { index i, j; set_pointer p, q; edge e; E에 속한 m개의 이음선을 가중치의 비내림차순으로 정렬; F = emptyset; initial(n); while (F에 속한 이음선의 개수가 n-1보다 작다) { e = 아직 점검하지 않은 최소의 가중치를 가진 이음선; i, j = e를 이루는 양쪽 정점의 인덱스; p = find(i); q = find(j); if (!equal(p,q)) { merge(p,q); e를 F에 추가; }}} |
||
[Algorithm] 버블 정렬 (Bubble Sort)
[Algorithm] 버블 정렬 (Bubble Sort)
개 념여러 개의 자료 중에서 서로 이웃하는 키 값을 두 개씩 비교하여 순서를 결정하는 정렬 방법 I. 버블 정렬 (Bubble Sort)의 개요 가. 버블 정렬의 정의- 여러 개의 자료 중에서 서로 이웃
infoofit.tistory.com
[Algorithm] 삽입 정렬 (Insert Sort)
[Algorithm] 삽입 정렬 (Insert Sort)
개념첫번째 키는 정의된 것으로 보고 두번째 키부터 순서에 맞는 위치에 삽입시켜 정렬하는 방법 I. 삽입 정렬 (Insert Sort)의 개요 가. 삽입 정렬의 정의- 첫번째 키는 정의된 것으로 보고 두
infoofit.tistory.com
반응형